Comparación entre el modelo SVAR50_4B y SVAR50_AR1

Introducción

El objetivo de este documento es comparar concretamente los principales resultados de comparar el modelo SVAR50_4B y una variación del modelo con una matriz de restricción diferente, que represente un proceso autoregresivo de orden 1 para cada una de las variables (SVAR50_AR1).

Metodología

Las especificaciones generales para ambos modelos son que, la realización de la evaluación es fuera de muestra. Las fechas con las que se modeló van desde 2005Q1 hasta 2023Q4.

Variables endógenas

Ambos modelos cuentan con las siguientes variables endógenas y con el mismo ordenamiento:

Tasa de Variación Interanual del PIB de EEUU: d4_ln_y_star
Tasa de Variación Interanual del Índice de Precios de Transables: d4_ln_ipei
Tasa de Interes de fondos federales: i_star
Inflacion No Subyacente Interanual: d4_ln_cpi_nosub
Tasa de Variación Interanual del PIB de Guatemala: d4_ln_y
Inflación Subyacente Optima MSE Interanual: d4_ln_cpi_sub
Tasa de Variación Interanual del Tipo de Cambio Nominal: d4_ln_s
Tasa de Variación Interanual de la Base Monetaria: d4_ln_bm
Tasa de Interes Lider de Politica Monetaria: i

Variables objetivo:

Tasa de Variación Interanual del PIB de Guatemala: d4_ln_y
Inflación Subyacente Optima MSE Interanual: d4_ln_cpi_sub
Tasa de Variación Interanual del Tipo de Cambio Nominal: d4_ln_s
Tasa de Interes Lider de Politica Monetaria: i

Matriz de restricción de SVAR50_4B

La principal distinción entre modelos es la matriz de restricciones para el modelo SVAR50_4B es \[ \small \begin{pmatrix} NaN& NaN&0 & 0& 0& 0& 0& 0& 0& 0\\ NaN& 0& NaN& 0& 0& 0& 0& 0& 0& 0\\ NaN& 0& 0& NaN& 0& 0& 0& 0& 0& 0\\ NaN& 0& 0& 0& NaN& 0& 0& 0& NaN& 0\\ NaN& 0& 0& 0& 0& NaN& 0& 0& NaN& 0\\ NaN& 0& NaN& 0& 0& 0& 0.9& 0& NaN& 0\\ NaN& 0& 0& 0& 0& 0& 0& NaN& NaN& NaN\\ NaN& 0& 0& 0& NaN& 0& 0& 0& NaN& NaN\\ NaN& 0& 0& NaN& NaN& 0& NaN& 0& NaN& NaN\\ \end{pmatrix} \] donde \(NaN\) son los parámetros libres que se estiman.

Matriz de restricción de SVAR50_AR1

Mientras que para el AR_1 es simplemente la matriz con la diagonal libre y ceros en el resto.

\[ \small \begin{pmatrix} NaN& NaN&0 & 0& 0& 0& 0& 0& 0& 0\\ NaN& 0& NaN& 0& 0& 0& 0& 0& 0& 0\\ NaN& 0& 0& NaN& 0& 0& 0& 0& 0& 0\\ NaN& 0& 0& 0& NaN& 0& 0& 0& 0& 0\\ NaN& 0& 0& 0& 0& NaN& 0& 0& 0& 0\\ NaN& 0& 0& 0& 0& 0& NaN& 0& 0& 0\\ NaN& 0& 0& 0& 0& 0& 0& NaN& 0& 0\\ NaN& 0& 0& 0& 0& 0& 0& 0& NaN& 0\\ NaN& 0& 0& 0& 0& 0& 0& 0& 0& NaN\\ \end{pmatrix} \]

Capacidad explicativa

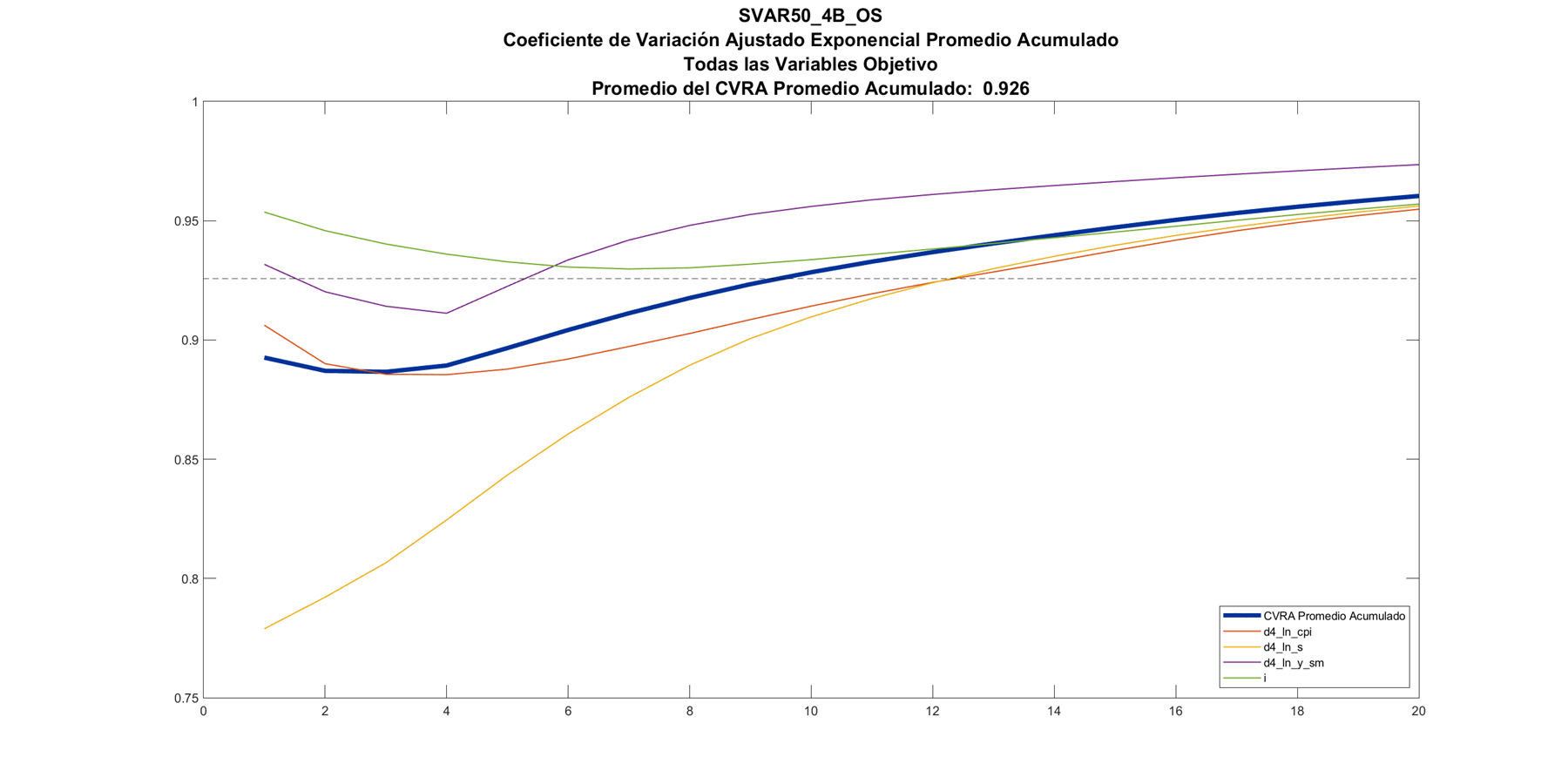
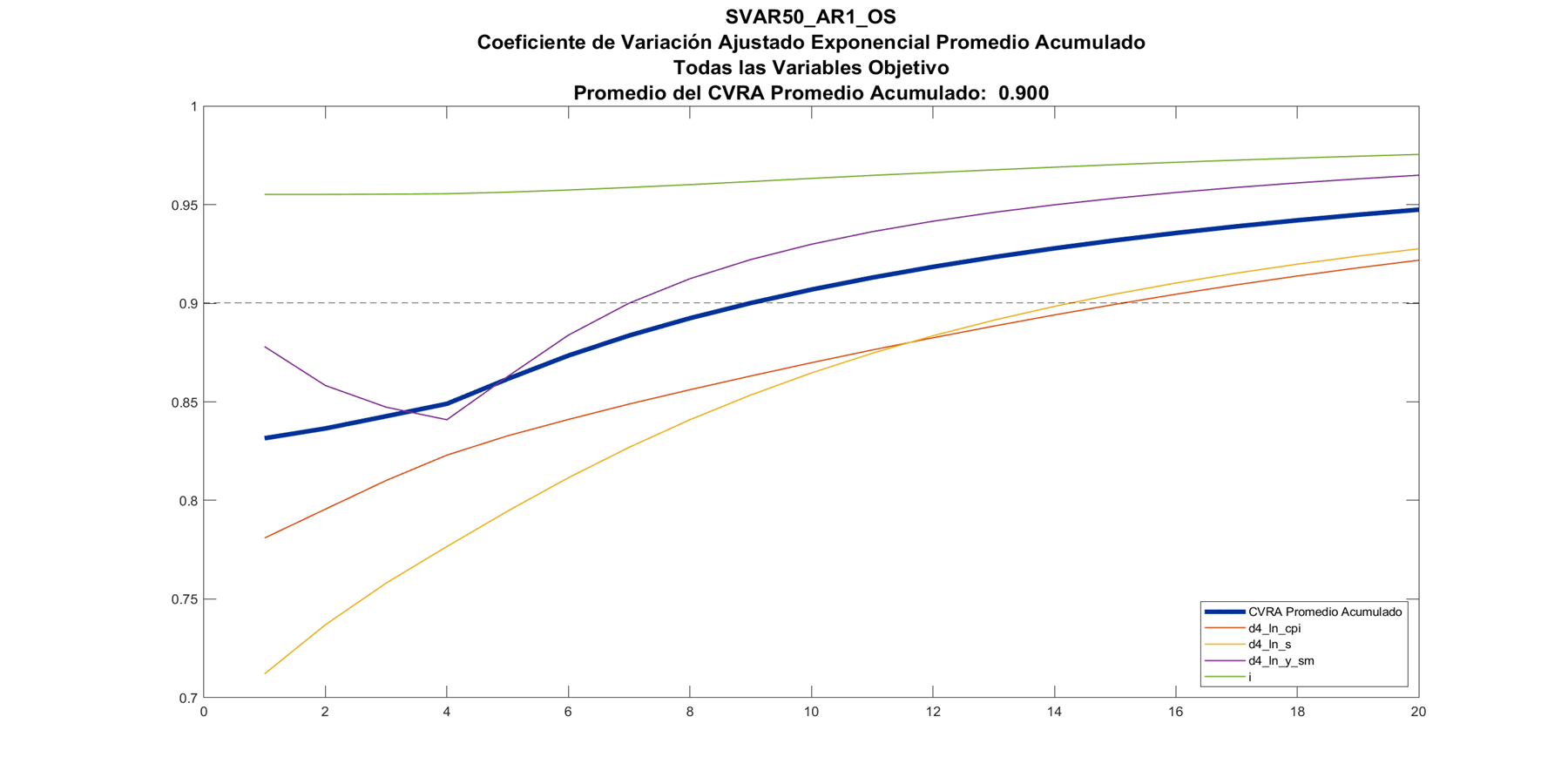
El promedio acumulada del coeficiente de variación de las variables objetivo, resulta ser menor en el modelo AR(1)

Capacidad predictiva

La función de perdida utilizada para medir la magnitud promedio de los errores de predicción es el RMSE de los errores en las submuestras por horizonte de las variable objetivo.

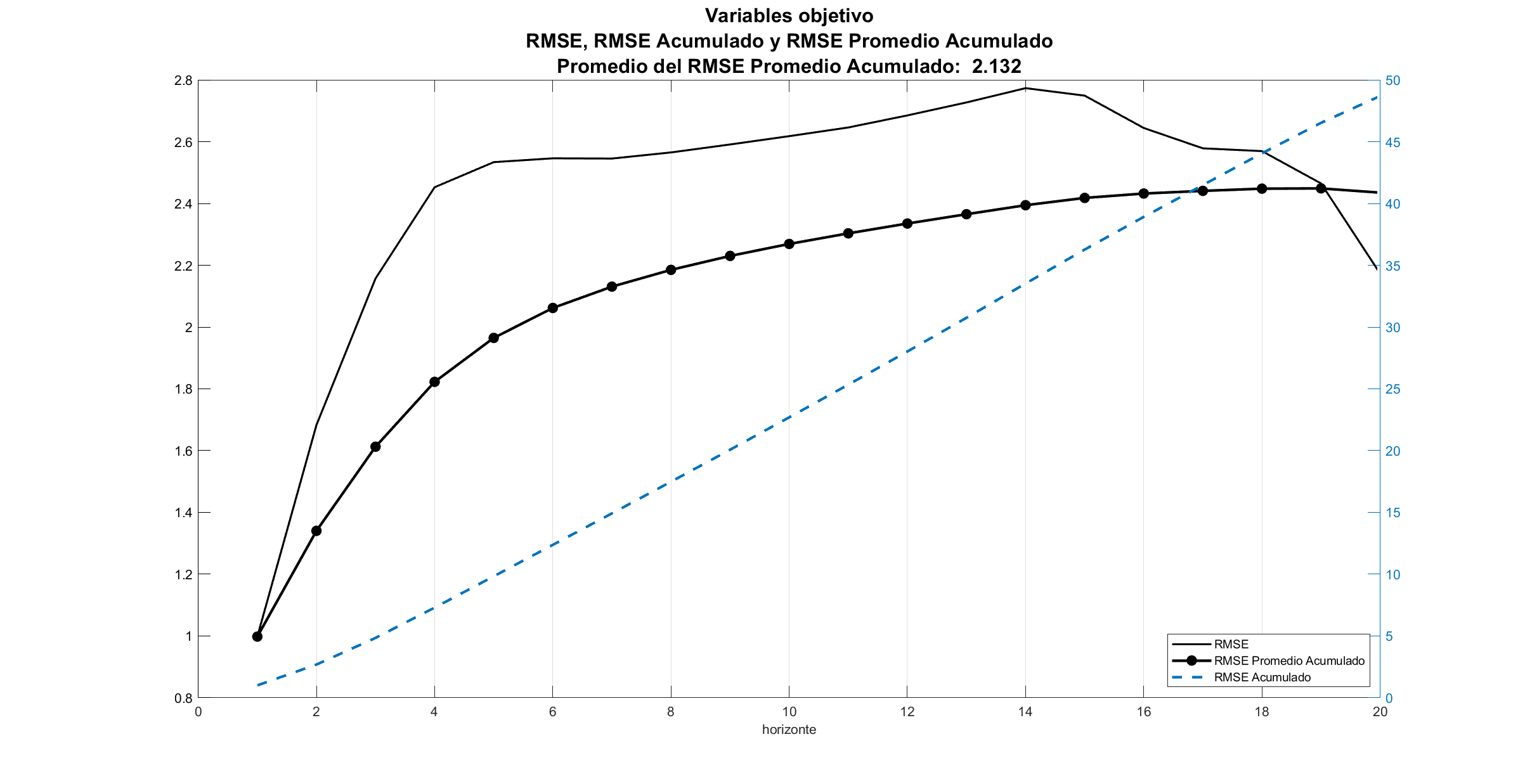
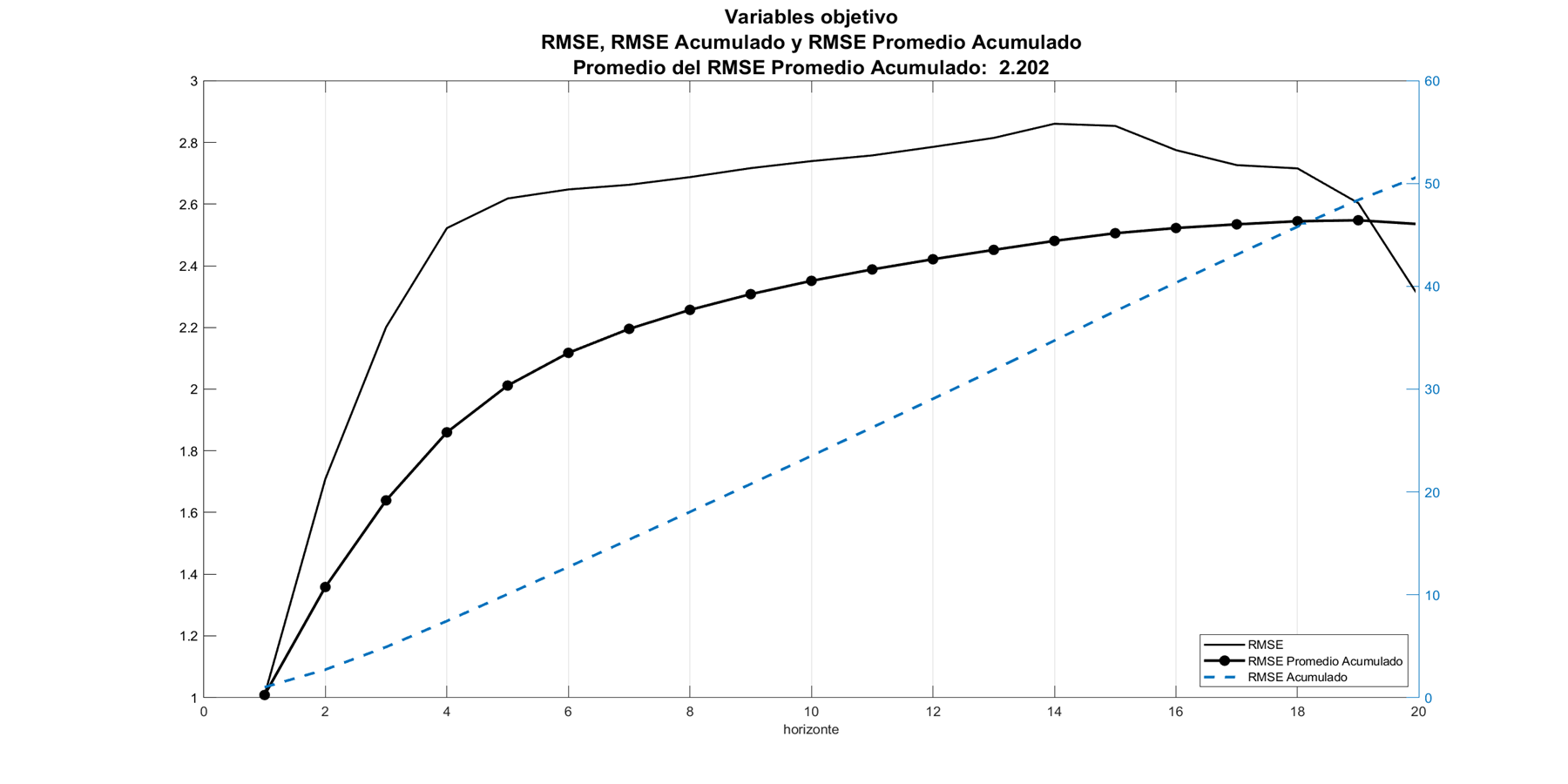
Cocientes entre resultados

Para comparar los resultados predictivos de ambos modelos se realiza un cociente de los resultados del SVAR50_4B entre los resultados del AR(1), por horizonte de cada una de las variables y se espera que el cociente sea menor a 1, lo que indicaría que los errores del AR(1) son mayores que los que se obtienen en el SVAR50_4B.

Resultados de los cocientes entre resultados
Horizontes	d4_ln_cpi	d4_ln_s	d4_ln_y_sm	i
1	0.894	1.108	0.983	0.828
2	0.905	1.087	0.966	0.840
3	0.922	1.066	0.954	0.844
4	0.932	1.049	0.940	0.847
5	0.930	1.039	0.948	0.841
6	0.922	1.034	0.968	0.821
7	0.920	1.031	0.986	0.793
8	0.928	1.025	1.007	0.765
9	0.926	1.025	1.019	0.755
10	0.925	1.036	1.014	0.763
11	0.923	1.048	1.001	0.789
12	0.927	1.052	0.986	0.819

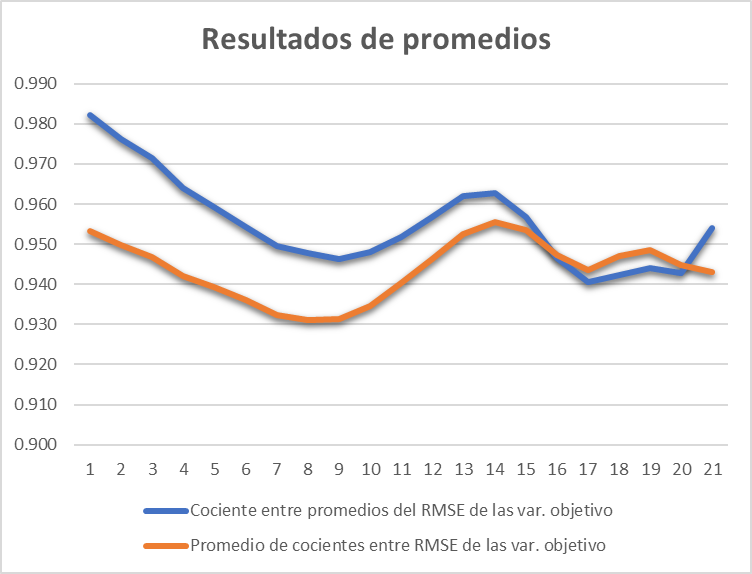
Cocientes promedios

En la mayoría de variables el cociente es menor a 1, excepto en el tipo de cambio.

Resultados de promedios
Horizontes	Cociente entre promedios del RMSE de las var. objetivo	Promedio de cocientes entre RMSE de las var. objetivo
1	0.982	0.953
2	0.976	0.950
3	0.971	0.947
4	0.964	0.942
5	0.959	0.939
6	0.954	0.936
7	0.950	0.932
8	0.948	0.931
9	0.946	0.931
10	0.948	0.935
11	0.952	0.940
12	0.957	0.946

En ambos promedio el cociente es menor a la unidad.

Presentación

Fullscreen ⛶